DiceCTF 2021: Lost in Your Eyes
Lost in Your Eyes
Solved by: oneup, papa
Description
Your eyes are like a maze, and I hate mazes, so help me escape.
nc dicec.tf 31578
Initial
We connect to the service specified and get absolutely no output. Once we send a little bit of data, only then does the service send anything back:
:(
Reversing the service
Time to pop it into IDA. There aren’t very many functions except for one huge one that immediately grabs our attention at 0x1420:
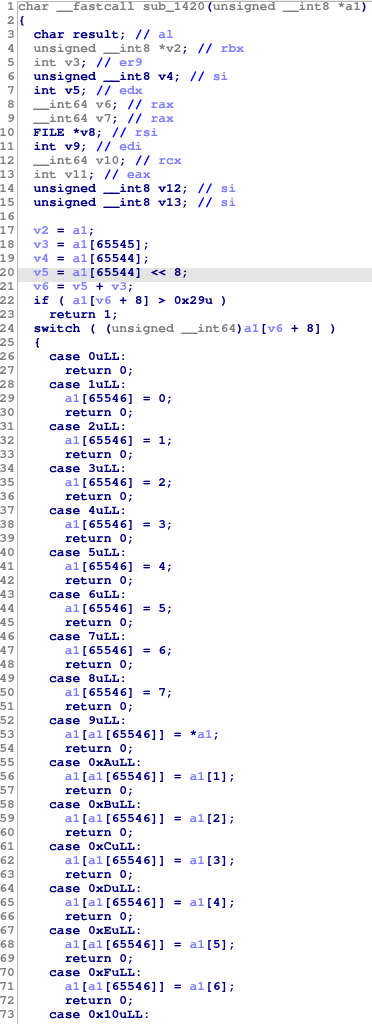
Virtual machine
From the giant switch statement, it looks like we’re dealing with some kind of homebrew VM here. The opcodes are pretty short and sweet and we can quickly determine the overall machine structure.
Registers:
- R0-R7: General purpose registers. R0 and R1 are also generally used for memory addresses and R6 and R7 are used for binary operations.
- RNDX: An index register that can be used to select one of R0-R7.
- PC: 16-bit register denoting current program location.
- UNK: Some unknown register that can be saved and restored, or set to one of four specific values.
Opcodes:
00: nop01-08: RNDX = <opcode> - 0109-10: R[RNDX] = R<opcode - 09>11-12: {++, --}R[RNDX]13-17: R[RNDX] = R6 {+, -, *, /, %} R718-19: R[RNDX] = {~, -} R[RNDX]1A-1C: R[RNDX] = R6 {&, |, ^} R71D-1E: R[RNDX] = R6 {==, <} R71F: R0,R1 = PC; R2 = UNK20: skip 1 instruction if R[RNDX] & 121: R[RNDX] = MEM[R0,R1]22: MEM[R0,R1] = R[RNDX]23: PC = R0,R1; UNK = R224: R[RNDX] = getchar()25: putc(R[RNDX])26-29: UNK = <opcode> - 26- any other opcode ends the VM immediately
Finally, we can also reverse the ultimate goal needed to get the flag: make the VM print out the characters :) and the interpreter will open and display the flag.
The unknown register
But what does that unknown register do? It seems the main place that it’s used is in the PC update code in 0x18D0, called after each call to the interpreter step function 0x1420:

A careful look reveals something surprising: the two 8-bit halves of PC are updated independently! The bottom 8 bits don’t carry over into the top 8 when they overflow. And now looking at how that unknown register is used makes sense: value 0 decrements PC_LO each step, value 1 increments PC_HI each step, value 2 increments PC_LO each step, and value 3 decrements PC_HI each step.
This little wrinkle also has huge ramifications on the structure of this machine. Code is divided into 256-byte banks: reaching the end of one wraps you back to the beginning, it doesn’t proceed to the next one automatically. In some ways this is similar to segment registers in the original 8086, or memory banks in early game consoles like the NES or the Game Boy.
Disassembling
We also see a huge section of memory at 0x40A0 that is the initial memory of the VM. It’s divided into 0x70 chunks of 0x70 bytes, where 0x70 bytes get loaded to the beginning of one 0x100 bank, and then the next 0x70 bytes get loaded to the beginning of the next 0x100 bank. The remaining banks from 0x70-0x100 are also left empty.
Using this we can write a basic disassembler using the table above, giving us output like this:
BANK 0
0: PCSTEPMODE = INC_HI
1: PCSTEPMODE = DEC_LO
2: PCSTEPMODE = DEC_HI
3: R[NDX] = R6 * R7
4: NOP
5: NOP
6: PC = R0,R1 ; PCSTEPMODE = R2
7: ??? (0x3a)
8: PCSTEPMODE = INC_HI
9: R[NDX] = R1
10: PCSTEPMODE = DEC_LO
11: NOP
12: NOP
13: NOP
14: NOP
15: NOP
16: NOP
17: NOP
18: NOP
19: NOP
20: NOP
21: NOP
Better representation?
It’s a good start, but doesn’t really capture how easy it is to move from one bank to the next. After all, we might be stepping from 00:24 to 01:24 to 02:24 and it’s pretty hard to look through each bank finding the right instruction.
It’s almost like you can step horizontally through a bank or you can step vertically from bank to bank. Almost like some kind of two dimensional thing? Maybe this is where the problem description comes into play, referencing some kind of maze. So what does it look like if we draw the opcodes on a 2-D grid? We don’t have enough room to spell out whole instructions in 2-D, but we can put in some short mnemonics for a few opcodes, like arrow characters for the opcodes that set the STEPMODE register. We code it up real fast and suddenly we see:
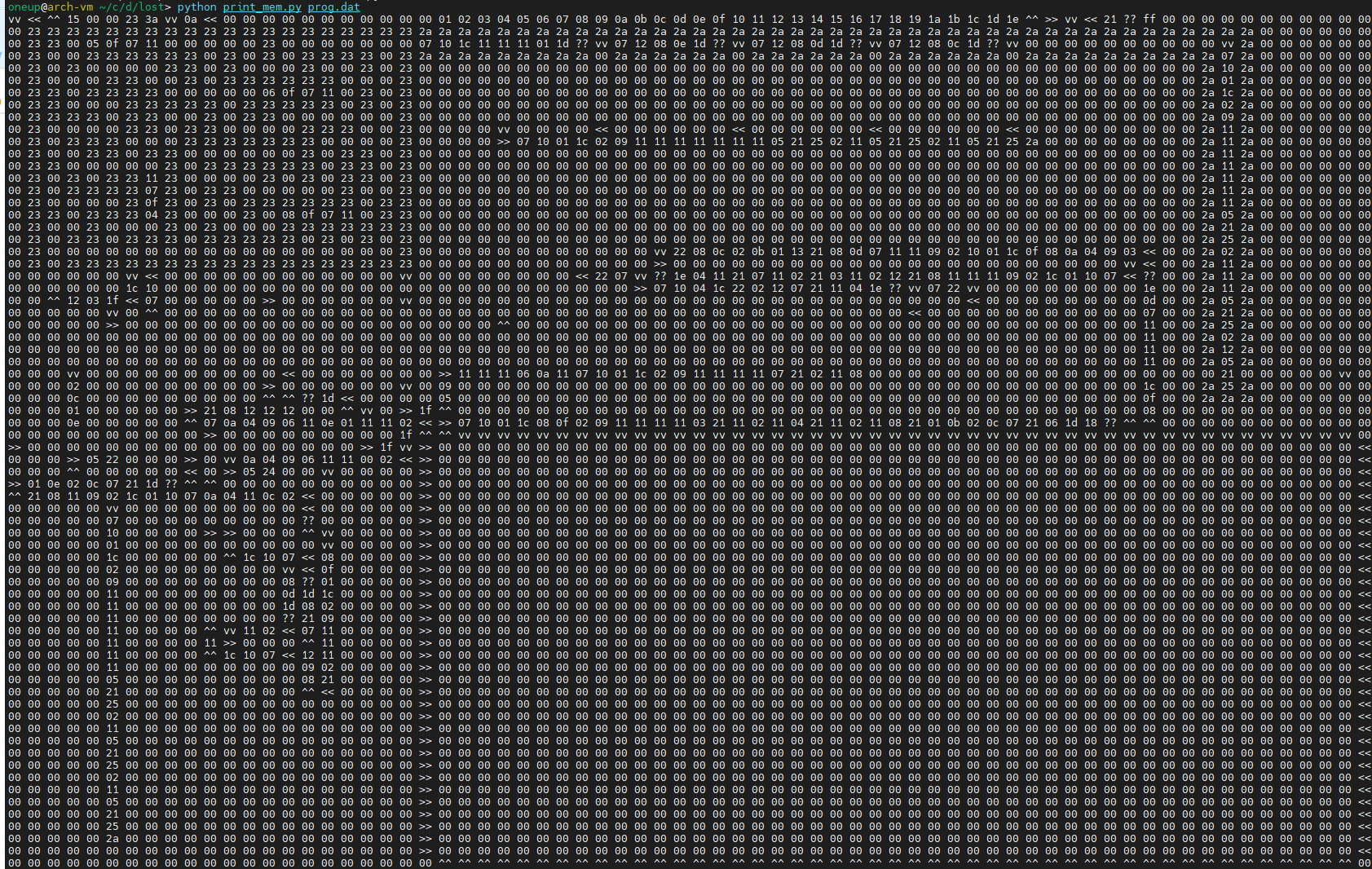
Whoa. Now we’re getting somewhere.
Hey, speaking of mazes, is it just me or is that a maze in the top left corner?
Emulation
But we still don’t know a whole lot about what the program is doing, or what input it’s looking for. Let’s write a quick little emulator to get some dynamic introspection to see what’s going on:
[ 0, 0] [ ,+] [00] 00 00 00 00 00 00 00 28 PCSTEPMODE = v
[ 1, 0] [+, ] [00] 00 00 00 00 00 00 00 00 NOP
[ 2, 0] [+, ] [00] 00 00 00 00 00 00 00 00 NOP
[ 3, 0] [+, ] [00] 00 00 00 00 00 00 00 00 NOP
...snip...
[23, 0] [+, ] [00] 00 00 00 00 00 00 00 27 PCSTEPMODE = >
[23, 1] [ ,+] [00] 00 00 00 00 00 00 00 00 NOP
[23, 2] [ ,+] [00] 00 00 00 00 00 00 00 00 NOP
...snip...
[23,12] [ ,+] [00] 00 00 00 00 00 00 00 27 PCSTEPMODE = >
[23,13] [ ,+] [00] 00 00 00 00 00 00 00 1f R0,R1 = PC ; R2 = PCSTEPMODE
[23,14] [ ,+] [23] 13 01 00 00 00 00 00 28 PCSTEPMODE = v
[24,14] [+, ] [23] 13 01 00 00 00 00 00 29 PCSTEPMODE = <
[24,13] [ ,-] [23] 13 01 00 00 00 00 00 02 NDX = 1
[24,12] [ ,-] 23 [13] 01 00 00 00 00 00 00 NOP
[24,11] [ ,-] 23 [13] 01 00 00 00 00 00 11 ++R[NDX]
[24,10] [ ,-] 23 [14] 01 00 00 00 00 00 11 ++R[NDX]
[24, f] [ ,-] 23 [15] 01 00 00 00 00 00 06 NDX = 5
[24, e] [ ,-] 23 15 01 00 00 [00] 00 00 09 R[NDX] = R0
It’s still a LOT of stuff to go through, but now we can see a whole lot better what’s going on.
Finding the right input
Setting the input to be ‘xyz’, we can run the emulator and see where it rejects our input. Thankfully it’s not too hard to find: the last 40 or so instructions look like this:
[2a, b] [-, ] 00 3b 01 15 78 23 [00] 01 27 PCSTEPMODE = >
[2a, c] [ ,+] 00 3b 01 15 78 23 [00] 01 00 NOP
[2a, d] [ ,+] 00 3b 01 15 78 23 [00] 01 00 NOP
[2a, e] [ ,+] 00 3b 01 15 78 23 [00] 01 00 NOP
[2a, f] [ ,+] 00 3b 01 15 78 23 [00] 01 26 PCSTEPMODE = ^
[29, f] [-, ] 00 3b 01 15 78 23 [00] 01 20 IF NOT (R[NDX] & 1)
[28, f] [-, ] 00 3b 01 15 78 23 [00] 01 29 PCSTEPMODE = <
[28, e] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, d] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, c] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, b] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, a] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, 9] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, 8] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, 7] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, 6] [ ,-] 00 3b 01 15 78 23 [00] 01 00 NOP
[28, 5] [ ,-] 00 3b 01 15 78 23 [00] 01 28 PCSTEPMODE = v
[29, 5] [+, ] 00 3b 01 15 78 23 [00] 01 07 NDX = 6
[2a, 5] [+, ] 00 3b 01 15 78 23 [00] 01 10 R[NDX] = R7
[2b, 5] [+, ] 00 3b 01 15 78 23 [01] 01 01 NDX = 0
[2c, 5] [+, ] [00] 3b 01 15 78 23 01 01 1c R[NDX] = R6 ^ R7
[2d, 5] [+, ] [00] 3b 01 15 78 23 01 01 02 NDX = 1
[2e, 5] [+, ] 00 [3b] 01 15 78 23 01 01 09 R[NDX] = R0
[2f, 5] [+, ] 00 [00] 01 15 78 23 01 01 11 ++R[NDX]
[30, 5] [+, ] 00 [01] 01 15 78 23 01 01 11 ++R[NDX]
[31, 5] [+, ] 00 [02] 01 15 78 23 01 01 11 ++R[NDX]
[32, 5] [+, ] 00 [03] 01 15 78 23 01 01 11 ++R[NDX]
[33, 5] [+, ] 00 [04] 01 15 78 23 01 01 11 ++R[NDX]
[34, 5] [+, ] 00 [05] 01 15 78 23 01 01 11 ++R[NDX]
[35, 5] [+, ] 00 [06] 01 15 78 23 01 01 11 ++R[NDX]
[36, 5] [+, ] 00 [07] 01 15 78 23 01 01 05 NDX = 4
[37, 5] [+, ] 00 07 01 15 [78] 23 01 01 21 R[NDX] = MEM[R0,R1]
[38, 5] [+, ] 00 07 01 15 [3a] 23 01 01 25 PUTC(R[NDX])
:[39, 5] [+, ] 00 07 01 15 [3a] 23 01 01 02 NDX = 1
[3a, 5] [+, ] 00 [07] 01 15 3a 23 01 01 11 ++R[NDX]
[3b, 5] [+, ] 00 [08] 01 15 3a 23 01 01 05 NDX = 4
[3c, 5] [+, ] 00 08 01 15 [3a] 23 01 01 21 R[NDX] = MEM[R0,R1]
[3d, 5] [+, ] 00 08 01 15 [28] 23 01 01 25 PUTC(R[NDX])
([3e, 5] [+, ] 00 08 01 15 [28] 23 01 01 02 NDX = 1
[3f, 5] [+, ] 00 [08] 01 15 28 23 01 01 11 ++R[NDX]
[40, 5] [+, ] 00 [09] 01 15 28 23 01 01 05 NDX = 4
[41, 5] [+, ] 00 09 01 15 [28] 23 01 01 21 R[NDX] = MEM[R0,R1]
[42, 5] [+, ] 00 09 01 15 [0a] 23 01 01 25 PUTC(R[NDX])
[43, 5] [+, ] 00 09 01 15 [0a] 23 01 01 2a END
There’s the :( being printed out. And R4 has the first character of our input, ‘x’. Stepping back some more, we see that it’s searching a table at 00:15 for each character of our input to see if it’s in the table.
So what’s in the table?
00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f 10 11 12 13 14 15 16 17 18 19 1a 1b 1c 1d 1e 26 27 28 29 21 20
Hmm… those are almost the same bytes that are valid opcodes…
So let’s set our input to \x01\x02\x03\x04 + (\x00 * 0x1000) and run it to see if we can get further.
But now it’s looping endlessly, WTF? It seems to be bouncing back and forth between 22:44 and 45:44, executing a string of 00 for all eternity:
[22,44] [-, ] 00 05 01 16 23 16 00 [00] 28 PCSTEPMODE = v
[23,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[24,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[25,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[26,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[27,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[28,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[29,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2a,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2b,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2c,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2d,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2e,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2f,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[30,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[31,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[32,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[33,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[34,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[35,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[36,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[37,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[38,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[39,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3a,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3b,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3c,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3d,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3e,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3f,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[40,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[41,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[42,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[43,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[44,44] [+, ] 00 05 01 16 23 16 00 [00] 00 NOP
[45,44] [+, ] 00 05 01 16 23 16 00 [00] 26 PCSTEPMODE = ^
[44,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[43,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[42,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[41,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[40,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3f,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3e,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3d,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3c,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3b,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[3a,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[39,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[38,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[37,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[36,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[35,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[34,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[33,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[32,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[31,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[30,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2f,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2e,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2d,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2c,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2b,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[2a,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[29,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[28,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[27,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[26,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[25,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[24,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[23,44] [-, ] 00 05 01 16 23 16 00 [00] 00 NOP
[22,44] [-, ] 00 05 01 16 23 16 00 [00] 28 PCSTEPMODE = v
Wait a second… didn’t we give it a long string of 00 for our input? What happens if we change it to 01?
[22,44] [-, ] [00] 05 01 16 23 16 00 00 28 PCSTEPMODE = v
[23,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
[24,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
[25,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
[26,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
[27,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
[28,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
[29,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
[2a,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
[2b,44] [+, ] [00] 05 01 16 23 16 00 00 01 NDX = 0
Sure enough, it looks like we’re giving it a program to execute. Some more inspection reveals that our input is being used to fill the giant box in the lower right corner of the memory map above:

Escaping the box
So now we can compare the table mentioned earlier to the actual opcode list and see which opcodes we’re prohibited from using:
- 1F:
R0,R1 = PC; R2 = STEPMODE - 22:
MEM[R0,R1] = R[RNDX] - 23:
PC = R0,R1; STEPMODE = R2 - 24:
R[RNDX] = getchar() - 25:
putc(R[RNDX])
So we can’t do console I/O, we can’t write to memory, and we can’t jump. Then how do we escape the box? There must be some way out. And indeed, examining the top left corner reveals that there is a 1-instruction gap we can fit through.
(Interesting tangent: If you look through the interpreter code for the conditional skip, you’ll find there’s quite a bit of code added to make sure you’re not skipping an instruction that sets STEPMODE to be 180 degrees from the direction you’re traveling. Our suspicion, which was later confirmed by the organizers, was that this was to make sure you didn’t “hop” the outer wall of the box by conditionally skipping the instruction that sent you back into the box.)
Reaching the maze
Time to reverse what all is going on in the opcodes where you can leave the jail.
insert montage here
Basically, each time you exit the jail, it iterates over one character in the maze. If the current character is not 23 (far jump), then it will overwrite the current character based on the value you loaded into R4 before exiting:
- 00:
^^ - 01:
>> - 02:
vv - 03:
<<
Once it’s iterated over the whole maze, it will transfer execution to it. There’s also 4 snippets included as part of the maze:
04 0F 07 11:RNDX = 3; R[RNDX] = R6; RNDX = 6; ++R[RNDX](R3 = R6++)05 0F 07 11:RNDX = 4; R[RNDX] = R6; RNDX = 6; ++R[RNDX](R4 = R6++)06 0F 07 11:RNDX = 5; R[RNDX] = R6; RNDX = 6; ++R[RNDX](R5 = R6++)08 0F 07 11:RNDX = 7; R[RNDX] = R6; RNDX = 6; ++R[RNDX](R7 = R6++)
There’s code after the maze that checks that we exit the maze with
R3 = 0 | R4 = 1 | R5 = 2 | R7 = 3
so we need to make sure we our path through the maze hits those 4 snippets in the order listed above.
If we make it through the maze with those register values, then finally we get to a region of code that prints out :), which will trigger the interpreter to give us our flag.
Final program
So now all we need is a program that will load R4 with the right values when we exit the maze. Thankfully the maze loading code leaves the current maze position in R6:R7 when it returns execution to our code. So we can just include our own 2-D copy of the values we want copied over to the maze, then write a series of instructions along the frame to translate R6:R7 to index into our program and use that to load R4:


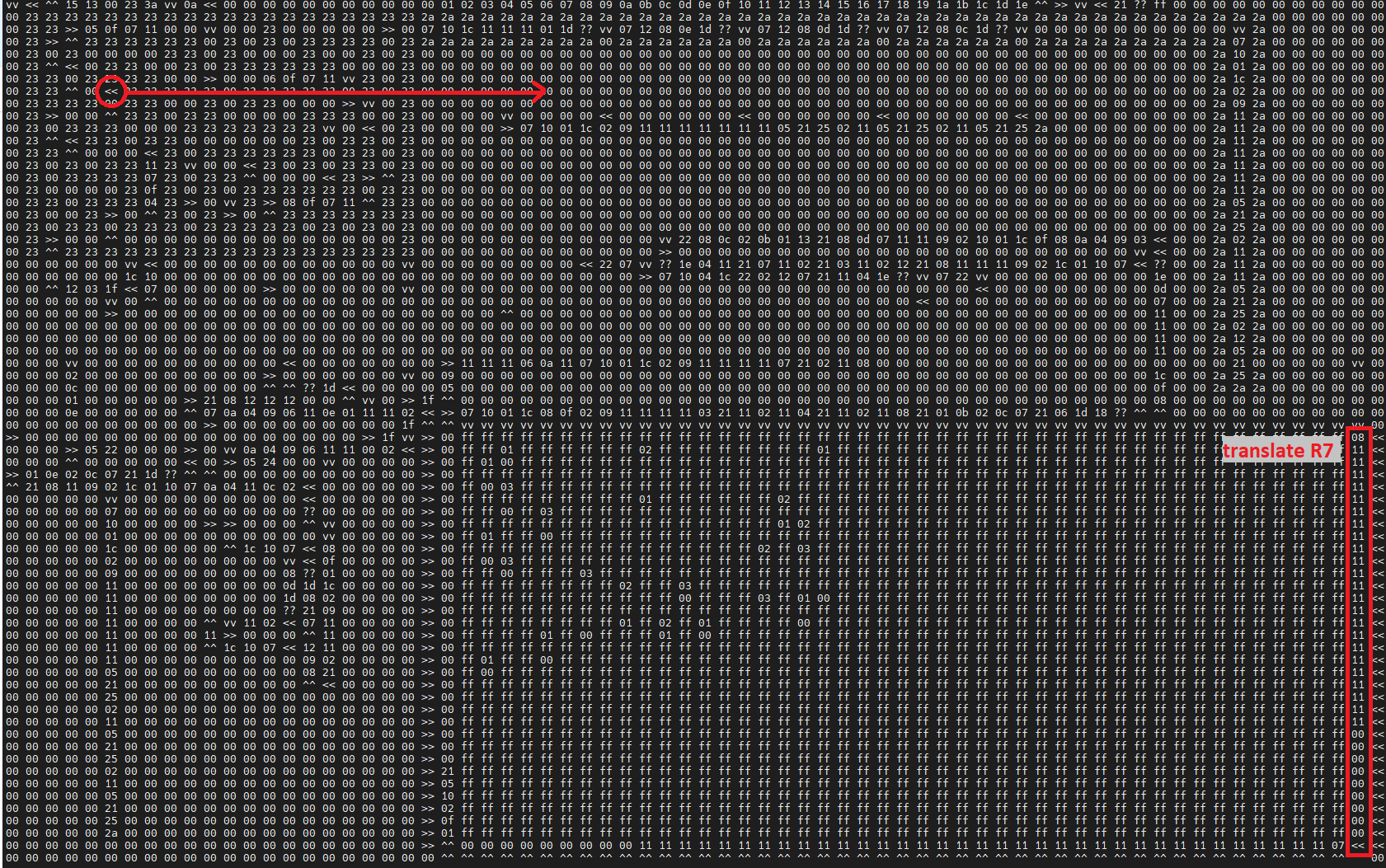


Flag
Send the program to the service and we get the flag:
$ python solve.py
[+] Opening connection to dicec.tf on port 31578: Done
:)
dice{2d_vms_ar3_tw1c3_the_d_of_1d_vms}